La tercera ley de Newton establece lo siguiente:
Siempre
que un objeto ejerce una fuerza sobre un segundo objeto, el segundo
objeto ejerce una fuerza de igual magnitud y dirección opuesta sobre el
primero. Con frecuencia se enuncia como "A cada acción siempre se opone
una reacción igual". En cualquier interacción hay un par de fuerzas de
acción y reacción, cuya magnitud es igual y sus direcciones son
opuestas. Las fuerzas se dan en pares, lo que significa que el par de
fuerzas de acción y reacción forman una interacción entre dos objetos.
La tercera ley de Newton explica
las fuerzas de acción y reacción. Estas fuerzas las
ejercen todos los cuerpos que están en contacto con otro,
así un libro sobre la
mesa ejerce una fuerza de
acción sobre la mesa y la mesa una fuerza de
reacción sobre el libro. Estas fuerzas son iguales pero
contrarias; es decir tienen el mismo modulo y sentido, pero son
opuestas en direcion
Esto significa que siempre en que un cuerpo ejerce una fuerza
sobre otro este también ejerce una fuerza sobre
él.
Se nombra fuerza de acción a la que es ejercida por el
primer cuerpo que origina una fuerza sobre otro, por lo tanto se
denomina fuerza de reacción a la es originada por el
cuerpo que recibe y reacciona (De allí el nombre) con esta
otra fuerza sobre el primer cuerpo.
¿Pero qué pasa cuando ningún cuerpo origino
primariamente la fuerza, como en el ejemplo del libro sobre la
mesa? Cualquiera puede ser denominada fuerza de acción y
obviamente a la otra se le denominará como fuerza de
reacción.

Tercera ley de Newton o Ley de acción y reacción
La tercera ley de Newton es completamente original (pues las dos primeras ya habían sido propuestas de otras maneras) y hace de las leyes de la mecánica un conjunto lógico y completo. Expone que por cada fuerza que actúa sobre un cuerpo ,
este realiza una fuerza de igual intensidad, pero de sentido contrario
sobre el cuerpo que la produjo. Dicho de otra forma, las fuerzas,
situadas sobre la misma recta, siempre se presentan en pares de igual
magnitud y de dirección, pero con sentido opuesto.
Este principio presupone que la interacción entre dos partículas se
propaga instantáneamente en el espacio (lo cual requeriría velocidad
infinita), y en su formulación original no es válido para fuerzas
electromagnéticas puesto que estas no se propagan por el espacio de modo
instantáneo sino que lo hacen a velocidad finita "c".
Es importante observar que este principio de acción y reacción
relaciona dos fuerzas que no están aplicadas al mismo cuerpo,
produciendo en ellos aceleraciones diferentes, según sean sus masas. Por
lo demás, cada una de esas fuerzas obedece por separado a la segunda
ley. Junto con las anteriores leyes, ésta permite enunciar los
principios
Generalizaciones
Después de que Newton formulara las tres famosas leyes, numerosos
físicos y matemáticos hicieron contribuciones para darles una forma más
general o de más fácil aplicación a sistemas no inerciales o a sistemas. Una de estas primeras generalizaciones fue el 1743que era una forma válida para cuando existieran ligaduras que permitía
resolver las ecuaciones sin necesidad de calcular explícitamente el
valor de las reacciones asociadas a dichas ligaduras.
Por la misma época encontró una forma válida para cualquier sistema de referencia inercial o no-inercial sin necesidad de introducir . Ya que es un hecho conocido que las Leyes de Newton, tal como fueron escritas, sólo son válidas a los ,
o más precisamente, para aplicarlas a sistemas no-inerciales, requieren
la introducción de las llamadas fuerzas ficticias, que se comportan
como fuerzas pero no están provocadas directamente por ninguna partícula
material o agente concreto, s
Más tarde la introducción la obligó a modificar la forma de la segunda ley de Newton, y la dejó claro que las leyes de Newton o la relatividad general sólo son aproximaciones al comportamiento dinámico.
También se han conjeturado algunas modificaciones macroscópicas y
no-relativistas, basadas en otros supuestos como la dinámica
Generalizaciones relativistas
Las leyes de Newton constituyen tres principios aproximadamente
válidos para velocidades pequeñas. La forma en que Newton las formuló no
era la más general posible. De hecho la segunda y tercera leyes en su
forma original no son válidas Sin embargo formulados de forma ligeramente diferente la segunda ley es
válida, y la tercera ley admite una formulación menos restrictiva que
es válida en mecánica relativista.
- Primera ley, en ausencia de campos gravitatorios no requiere modificaciones. En un plano una línea recta cumple la condición de ser. En presencia de la primera ley de Newton sigue siendo correcta si sustituimos la expresión línea recta por línea geodésica.
- Segunda ley. Sigue siendo válida si se dice que la fuerza sobre una partícula coincide con la tasa de cambio.
Sin embargo, ahora la definición de momento lineal en la teoría
newtoniana y en la teoría relativista difieren. En la teoría newtoniana
el momento lineal se define segúnmientras que en la teoría de la relatividad de Einstein se define mediante
- donde m es la de partícula y
 la velocidad de ésta medida desde un cierto sistema inercial. Esta
segunda formulación de hecho incluye implícitamente definición
según la cual el momento lineal es el producto de la masa por la
velocidad. Como ese supuesto implícito no se cumple en el marco (donde la definición es ,
la expresión de la fuerza en términos de la aceleración en la teoría de
la relatividad toma una forma diferente. Por ejemplo, para el
movimiento rectilíneo de una partícula en un sistema inercial se tiene
que la expresión equivalente a es:
la velocidad de ésta medida desde un cierto sistema inercial. Esta
segunda formulación de hecho incluye implícitamente definición
según la cual el momento lineal es el producto de la masa por la
velocidad. Como ese supuesto implícito no se cumple en el marco (donde la definición es ,
la expresión de la fuerza en términos de la aceleración en la teoría de
la relatividad toma una forma diferente. Por ejemplo, para el
movimiento rectilíneo de una partícula en un sistema inercial se tiene
que la expresión equivalente a es:
(2b)
- Si la velocidad y la fuerza no son paralelas, la expresión sería la siguiente:
(2c)
- Nótese que esta última ecuación implica que salvo para el movimiento rectilíneo y el vector de aceleración y el vector de fuerza no serán parelelos y
formarán un pequeño ángulo relacionado con el ángulo que formen la
aceleración y la velocidad.
- Tercera Ley de Newton. La formulación original de la tercera
ley por parte de Newton implica que la acción y reacción, además de ser
de la misma magnitud y opuestas, son colineales. En esta forma la
tercera ley no siempre se cumple en presencia de campos magnéticos. En
particular, lade laque se ejercen dos partículas en movimiento no son iguales y de signo
contrario. Esto puede verse por cómputo directo. Dadas dos partículas
puntuales con cargas q1 y q2 y velocidades
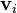 , la fuerza de la partícula 1 sobre la partícula 2 es:
, la fuerza de la partícula 1 sobre la partícula 2 es:

donde d la distancia entre las dos partículas y 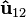 es el vector director unitario que va de la partícula 1 a la 2.
Análogamente, la fuerza de la partícula 2 sobre la partícula 1 es:
es el vector director unitario que va de la partícula 1 a la 2.
Análogamente, la fuerza de la partícula 2 sobre la partícula 1 es:

Empleando la identidad vectorial 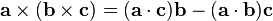 , puede verse que la primera fuerza está en el plano formado por
, puede verse que la primera fuerza está en el plano formado por 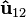 y
y  que la segunda fuerza está en el plano formado por
que la segunda fuerza está en el plano formado por 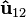 y
y 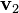 . Por tanto, estas fuerzas no siempre resultan estar sobre la misma línea, aunque son de igual magnitud (siempre que
. Por tanto, estas fuerzas no siempre resultan estar sobre la misma línea, aunque son de igual magnitud (siempre que 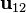 no sea paralela a
no sea paralela a  o
o 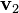 , ya que entonces ni siquiera se cumpliría la forma débil.)
, ya que entonces ni siquiera se cumpliría la forma débil.)
Versión débil de ley de acción y reacción
Como se explicó en la sección anterior ciertos sistemas magnéticos no
cumplen el enunciado fuerte de esta ley (tampoco lo hacen las fuerzas
eléctricas ejercidas entre una carga puntual y un dipolo). Sin embargo
si se relajan algo las condiciones los anteriores sistemas sí cumplirían
con otra formulación más débil o relajada de la ley de acción y
reacción. En concreto los sistemas descritos que no cumplen la ley en su
forma fuerte, si cumplen la ley de acción y reacción en su forma débil:
Todas las fuerzas de la mecánica clásica y el electromagnetismo
no-relativista cumplen con la formulación débil, si además las fuerzas
están sobre la misma línea entonces también cumplen con la formulación
fuerte de la tercera ley de Newton.

 la velocidad de ésta medida desde un cierto sistema inercial. Esta
segunda formulación de hecho incluye implícitamente definición
según la cual el momento lineal es el producto de la masa por la
velocidad. Como ese supuesto implícito no se cumple en el marco (donde la definición es ,
la expresión de la fuerza en términos de la aceleración en la teoría de
la relatividad toma una forma diferente. Por ejemplo, para el
movimiento rectilíneo de una partícula en un sistema inercial se tiene
que la expresión equivalente a es:
la velocidad de ésta medida desde un cierto sistema inercial. Esta
segunda formulación de hecho incluye implícitamente definición
según la cual el momento lineal es el producto de la masa por la
velocidad. Como ese supuesto implícito no se cumple en el marco (donde la definición es ,
la expresión de la fuerza en términos de la aceleración en la teoría de
la relatividad toma una forma diferente. Por ejemplo, para el
movimiento rectilíneo de una partícula en un sistema inercial se tiene
que la expresión equivalente a es:

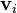 , la fuerza de la partícula 1 sobre la partícula 2 es:
, la fuerza de la partícula 1 sobre la partícula 2 es:
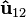 es el vector director unitario que va de la partícula 1 a la 2.
Análogamente, la fuerza de la partícula 2 sobre la partícula 1 es:
es el vector director unitario que va de la partícula 1 a la 2.
Análogamente, la fuerza de la partícula 2 sobre la partícula 1 es:
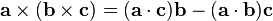 , puede verse que la primera fuerza está en el plano formado por
, puede verse que la primera fuerza está en el plano formado por  que la segunda fuerza está en el plano formado por
que la segunda fuerza está en el plano formado por 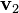 . Por tanto, estas fuerzas no siempre resultan estar sobre la misma línea, aunque son de igual magnitud (siempre que
. Por tanto, estas fuerzas no siempre resultan estar sobre la misma línea, aunque son de igual magnitud (siempre que 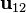 no sea paralela a
no sea paralela a
donde se aplica la tercera ley de newton?
ResponderEliminarse aplica es estos ejemplos:
ResponderEliminarSi una persona empuja a otra de peso similar, las dos se mueven pero en sentido contrario.
Cuando brincamos empujamos a la tierra hacia abajo y ésta nos empuja con la misma intensidad hacia arriba.
Una persona que rema en una lancha empuja el agua con el remo en una dirección y el agua responde empujando la lancha en dirección contraria.
Cuando caminamos empujamos a la tierra hacia atrás con nuestros pies, a lo cual la tierra responde empujándonos a nosotros hacia delante con la misma fuerza haciendo que avancemos.
La turbina de un avión ejerce una fuerza hacia atrás con el aire que suelta, lo cual ocasiona una reacción en sentido contrario y con la misma intensidad que hace que el avión avance hacia delante.
Cuando se dispara una bala, la explosión de la pólvora ejerce una fuerza sobre la pistola, la cual reacciona ejerciendo una fuerza de igual intensidad pero en sentido contrario sobre la bala.
Cuando se cuelga un objeto de una cuerda el objeto ejerce una fuerza hacia abajo, pero la cuerda ejerce una fuerza hacia arriba de igual intensidad, que hace que el objeto no se caiga.
La pólvora que se quema en el interior de un cohete al salir impulsa a la Tierra hacia abajo, generando una fuerza de la Tierra sobre el cohete que hace que éste vuele.
Cuando una persona salta de una lancha al muelle empuja la lancha hacia atrás y la lancha impulsa al hombre hacia adelante.
Al golpear un clavo con un martillo, el clavo ejerce una fuerza contraria que hace que el martillo revote hacia atrás.
Has despejado las dudas que tenia .. ! gracias , buen trabajo
ResponderEliminarde nada jejejejje :)
ResponderEliminarque es la acción y reación
ResponderEliminar