LA NOTACIÓN CIENTÍFICA
articulo:
la notación científica es muy útil para escribir números grandes y pequeños,esta escritura tiene una ventaja de ser mas concisa que la usual, se conforma en usar pocos dígitos significativos
la notación científica nos permite hacer cálculos mentales muy rápidos y también nos permite separar los dígitos significativos y el orden de magnitud
Un número está en notación científica si ha sido expresado en la forma a × 10b donde 1 <= a < 10 yb son enteros. La siguiente tabla presenta ejemplos de números y cómo ellos pueden ser expresados en notación científica. Cabe señalar que 2.34 EE4 es una notación abreviada para 2.34 x 104. En particular, este formato es común en las calculadoras.
| Número | Notación Científica | Forma EE de la Notación Científica |
| 123 | 1.23 × 102 | 1.23 EE 2 |
| 0.0234 | 2.34 × 10-2 | 2.34 EE -2 |
| 1230000 | 1.23 × 106 | 1.23 EE 6 |
| 0.000321 | 3.21 × 10-4 | 3.21 EE -4 |
El Efecto de las Potencias de 10
El objetivo de este tutorial es tomar los números en notación científica y presentarlos como números simples sin productos ni exponentes y tomar números simples y presentarlos en notación científica. La clave para hacerlo es comprender el efecto que tiene multiplicar un número por una potencia de diez. La manera más fácil de entender esto es asociar la multiplicación por potencias de diez con un movimiento del punto decimal.Las siguientes tablas muestran el efecto de multiplicar el número 1.23 por diversas potencias de 10. Cabe señalar que el número estará expresado como 1. 23000, para que el movimiento del punto decimal será más claro.
| Número | Potencia de 10 | Resultado | Movimiento del Punto Decimal |
| 1.23000 | × 100 | 1.23000 | 0 unidades a la derecha |
| 1.23000 | × 101 | 12.3000 | 1 unidad a la derecha |
| 1.23000 | × 102 | 123.000 | 2 unidades a la derecha |
| 1.23000 | × 103 | 1230.00 | 3 unidades a la derecha |
| 1.23000 | × 104 | 12300.0 | 4 unidades a la derecha |
| 1.23000 | × 105 | 123000. | 5 unidades a la derecha |
| Número | Potencia de 10 | Resultado | Movimiento del Punto Decimal |
| 1.23 | × 100 | 1.23000 |
0 unidades a la izquierda
|
| 1.23 | × 10-1 | 0.123 |
1 unidad a la izquierda
|
| 1.23 | × 10-2 | 0.0123 |
2 unidades a la izquierda
|
| 1.23 | × 10-3 | 0.00123 |
3 unidades a la izquierda
|
| 1.23 | × 10-4 | 0.000123 |
4 unidades a la izquierda
|
| 1.23 | × 10-5 | 0.0000123 |
5 unidades a la izquierda
|
- Eliminar todos los puntos decimales del número (en este caso no hay ningún punto decimal)473000
- Colocar un punto decimal en los dígitos para que el número esté entre uno y diez. En adelante nos referiremos a este número como a. En este caso a = 473000.
- Determinar el número de unidades y la dirección que el punto decimal debe moverse para convertir a al número inicial.
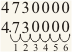
4.73000 a 4730000 significa 6 unidades a la derecha. - Consideraremos que el número b tiene la misma magnitud que el número de unidades que el punto decimal debe moverse y su signo es positivo si se mueve el punto decimal a la derecha y negativo si se mueve el punto decimal hacia la izquierda. En este caso b = +6
- El número en notación científica es a × 10b o en este caso 4.73000 × 106. Dependiendo de la situación, es usual eliminar los ceros de la derecha dando el resultado final
4.73 × 106.
CIFRAS SIGNIFICATIVAS
articulo:
* Cualquier dígito diferente de cero es significativo
* Los ceros situados en medio de números diferentes son significativos
* Los ceros a la izquierda del primer número distinto a cero no son significativos
* Para los números mayores que uno, los ceros escritos a la derecha de la coma decimal también cuentan como cifras significativas
En ocasiones hemos de utilizar números muy grandes, como la distancia en kilómetros de Saturno al Sol. O números muy pequeños, como el diámetro en cm. de un virus. El manejo de este tipo de números se simplifica utilizando potencias de 10 , o notación científica. En esta notación, el número se escribe como el producto de un número mayor o igual que 1 y menor estrictamente que 10 , y una potencia de 10 . Por ejemplo:100=
102=1⋅102 .72900=7,29⋅10000=7,29⋅104 .0,0000000065=6510000000000=65⋅10−10=6,5⋅10−9
Calcular, utilizando la notación científica, 230⋅9100 .
Observe cómo, en el último paso, se ha hecho una pequeña rectificación para que el número que multiplica a la potencia de 10 esté comprendido entre 1 y 10 , y así mostrar el resultado en notación científica.
Muchos de los resultados que se manejan en la ciencia son el resultado de una medida y por tanto sólo se conocen con cierta incertidumbre experimental. La magnitud de este error depende de la habilidad del experimentador y del aparato utilizado y frecuentemente sólo puede estimarse. Se suele dar una indicación aproximada de la incertidumbre de una medida mediante el número de dígitos que se utilice. Por ejemplo, si decimos que la longitud de una mesa es de 2,50 m. , queremos indicar que probablemente su longitud se encuentre entre 2,495 m. y 2,505 m. Si utilizamos un metro en el que se pueda apreciar el milímetro y medimos la longitud de la mesa cuidadosamente, podemos estimar que hemos medido esta misma longitud con una precisión de ±0,5 mm. en vez de ±0,5 cm. (véase el artículo dedicado a los números aproximados y a los errores, tanto absoluto como relativo, que se cometen al tomar los mismos como aproximación de un resultado o de una medida). Indicaríamos esta precisión utilizando cuatro dígitos, como por ejemplo 2,503 m. , para expresar la longitud. Recibe el nombre de cifra significativa todo dígito (exceptuando el cero cuando se utiliza para situar el punto decimal) cuyo valor se conoce con seguridad. El número 2,503 tiene cuatro cifras significativas. El número 0,00103 tiene tres cifras significativas; los tres primeros ceros no son cifras significativas ya que simplemente sitúan el punto decimal. En notación científica, este número se escribiría 1,03⋅10−3 . Un error muy común, sobre todo por el uso de las calculadoras, es arrastrar en el cálculo muchos más dígitos de los que en realidad se conocen. Supongamos, por ejemplo, que medimos el área de un recinto circular midiendo el radio en pasos y utilizando la fórmula del área A=πr2 . Si suponemos que un paso equivale, aproximadamente a 50 cm.=0,5 m. y estimamos que la longitud del radio es de 16 pasos, o sea, de 8 m. , utilizando una calculadora de diez dígitos para determinar el valor del área, obtenemos
Los dígitos situados detrás de la coma decimal no sólo dificultan el cálculo sino que inducen a confusión respecto a la exactitud con la que conocemos el área. Podríamos aproximar el resultado a 201 m.2 , pero ni siquiera esto es cierto. Si se ha calculado el radio mediante pasos la exactitud de la medida será tan sólo de 0,5 m. Es decir, la longitud del radio tendrá como máximo un valor de 8,5 m. y como mínimo un valor de 7,5 m. Si la longitud del radio es de 8,5 m. el valor del área es
Mientras que si la longitud del radio es de 7,5 m. , el área vale
Una regla general válida cuando se manejan diferentes números en una operación de multiplicación o división es que el número de cifras significativas del resultado no debe ser mayor que el menor número de cifras significativas de cualesquiera de los números. En este caso sólo se conoce una cifra significativa del radio, por tanto sólo se conoce una cifra significativa del área. Esta debe expresarse como 2⋅102 m.2 . Si en lugar de medir el radio mediante pasos se utiliza un metro y se obtiene un valor de, por ejemplo, r=8,23 m. , el área se expresará con tres cifras significativas:
Es muy habitual que los libros de texto de carácter científico trabajen generalmente con tres o cuatro cifras significativas.
Cuando se llevan a cabo cálculos por aproximación o comparaciones, hay veces en que se redondea un número hasta una e incluso ninguna cifra significativa. Por ejemplo, la altura de un pequeño insecto, digamos una hormiga, puede ser de 8⋅10−4 m.≈10−3 m. Diremos que el orden de magnitud de la altura de una hormiga es −3 o de 10−3 m. De igual modo, como la altura de la mayoría de las personas se encuentra próxima a 2 m. , podemos redondear este número y decir que el orden de magnitud de la altura de una persona es 0 o de 100 m.=1 m. Esto no quiere decir que la altura típica de una persona sea realmente de 1 m. sino que está más próxima a 1 m. que a 10 m. o 10−1=0,1 m. Podemos decir que una persona típica es 3 órdenes de magnitud más alta que una hormiga típica, queriendo decir con esto que el cociente entre las alturas es aproximadamente 103 .


No hay comentarios:
Publicar un comentario